Products & Solutions
NOGRID software FPM
NOGRID GmbH, a German Bodenheim based company, brings to market a revolutionary software for the simulation of flows: NOGRID FPM. FPM software is the first available commercial meshfree Computational Fluid Dynamics (CFD) code for simulation tasks in a wide area of flow and continuum mechanical problems.
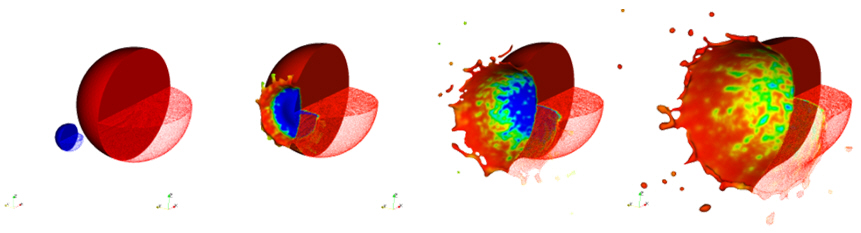
FPM is a meshfree method. The basis of the computations is a point cloud, which represents the continuum or in other words a continuum domain (fluid or solid) is replaced by a discrete number of points, which are referred to as finite points. Each finite point carries all fluid information, like density, velocity, pressure, temperature. Finite points can move with fluid velocity (Lagrangian approach) or the flow information runs through the finite points if they are located constant in space (Eulerian approach). Also a mixture approach (Arbitrary Lagrangian Eulerian ALE) is possible. This is useful in case of using the Eulerian approach in combination with free surfaces or moving parts. Therefore, finite points themselves can be considered as geometrical grids of the fluid domain.
The finite point density is prescribed by a smoothing length defined locally. FPM does not use a rigid neighbourhood list for a certain finite point as it is required in a mesh based method. All neighbours are allowed to move and the neighbourhood list is re-computed each time step. Thus the simple idea of FPM is to use a dynamical discretization method, but the finite points itself are carrying all fluid information.
This method has various advantages over grid-based techniques; for example, it can handle fluid domains, which change naturally, whereas grid based techniques require additional computational effort. The finite points have to completely cover the whole flow domain, i.e. the point cloud has to fulfill certain quality criteria (finite points are not allowed to form 'holes' which means finite points have to find sufficiently numerous neighbours; also, finite points are not allowed to cluster; etc.).
The finite point cloud is a geometrical basis, which allows for a numerical formulation making FPM a general finite difference idea applied to continuum mechanics. That especially means, if the point cloud would reduce to a regular cubic point grid, then FPM would reduce to a classical finite difference method. The idea of general finite differences also means that FPM is not based on a weak formulation like Galerkin's approach. Rather, FPM is a strong formulation which models differential equations by direct approximation of the occurring differential operators. The method used is a moving least squares idea which was especially developed for FPM.
Competitive advantages including:
Extremely short modelling time
Dramatically reduced computing time in case of free surface flows or flows with moving parts or moving boundaries
Easy data exchange to existing CFD/CAE environments
Direct import of models from CAD-Systems
Thinking CFD? Think FPM!
You can find more information about FPM software on www.nogrid.com.